It is possible to draw Bézier curves onto the canvas. To achieve this, we need to call the two methods related to drawing Bézier curves, namely: quadraticCurveTo() and bezierCurveTo().

  • quadraticCurveTo(cpx, cpy, epx, epy)

This method requires four arguments:

  1. cpx: the x-axis coordinate of the control point.
  2. cpy: the y-axis coordinate of the control point.
  3. epx: the x-axis coordinate of the end point.
  4. epy: the y-axis coordinate of the end point.

The starting point may be the latest point in the current path or it may be changed using the method moveTo().

index.js
const canvas = document.getElementById("canvas")
const context = canvas.getContext("2d")

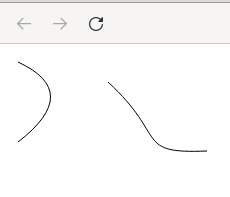
context.beginPath()
context.moveTo(10, 10) // Coordinates of the starting point (10, 10)
/*
Coordinates of the control point (75, 40) and
coordinates of the end point (10, 90)
*/
context.quadraticCurveTo(75, 40, 10, 90)
context.stroke() // stroke() must be called to draw the curve

quadratic curve

  • bezierCurveTo(cp1x, cp1y, cp2x, cp2y, epx, epy)

This cubic Bézier curve drawing method is similar to the previous one, except that two control points are required instead of one.

  1. cp1x: the x-axis coordinate of the first control point.
  2. cp1y: the y-axis coordinate of the first control point.
  3. cp2x: the x-axis coordinate of the second control point.
  4. cp2y: the y-axis coordinate of the second control point.
  5. epx: the x-axis coordinate of the end point.
  6. epy: the y-axis coordinate of the end point.
context.beginPath()
context.moveTo(100, 30)
context.bezierCurveTo(160, 85, 126, 102, 199, 99)
context.stroke()

bezier curve

There is a very interesting video on YouTube by Freya Holmér explaining the mathematics behind the Bézier curves: The Beauty of Bézier Curves